How to Prove It: A Structured Approach (3rd Edition) by Daniel Velleman is one of the main resources I’ve been using for the intro to math phase of my math learning project. It’s an excellent “intro to proofs” book suitable for self-study or for a course aimed at math majors making the transition to higher mathematics. How to Prove It is challenging enough—especially the many excellent exercises—that I think it would probably serve best for an honors version of such a course.1
Although I don’t remember where I first heard of How to Prove It (maybe the Math Sorcerer?), it’s a standard text, so anyone looking for a foundational introduction to proof writing will inevitably come across it. When I started my math learning project, my plan was to focus on Pure Mathematics for Beginners by Dr. Steve Warner, and indeed that has been my main breadth-first text, but I found Velleman’s book valuable enough that I ended up studying the whole thing.
And I mean studying—in addition to filling up an entire large Moleskin notebook, I also wrote up almost 400 pages of typeset notes. This included annotated and expanded version of proofs in the main text as well as a large number of problems. Possibly too large—there are so many excellent sequences of related exercises in How to Prove It that I often found them too tempting to resist. The result was that this intro phase of my math learning project took much longer than expected. On the other hand, the resulting foundation is much more solid than expected, and there were many more gaps and deficiencies in my background than I realized.
I should also note how valuable it was to have access to the solutions manual for the book. I could usually figure out proofs for the exercises on my own, but sometimes I’d get stuck. In some cases, a quick glance at the start of the solution would be enough to get me going again. In other cases, reading the solutions manual confirmed that I never would have gotten the answer on my own, and sometimes I’d have trouble understanding the proof even after studying the solution in detail. In such cases, copying the solution into my LATEX notes and supplying any missing justifications proved highly instructive.
1 Contents
If you have (as I did) what you might consider a reasonable background in mathematics, the chapter list in Velleman looks innocent enough:
Sentential Logic
Quantification Logic
Proofs
Relations
Functions
Mathematical Induction
Number Theory
Infinite Sets
Most of these topics I thought I basically understood. But time and again I’d come to a section, think, “OK, this will be pretty easy”, and then realize almost all the material was new to me.
For example, consider Chapter 4, Relations. I’d heard of relations before, and so was surprised to learn that in fact I had no idea what they really were. I also discovered in Chapter 5, Functions, that—despite years of using functions—I didn’t really know what those were, either.
2 What is a function?
To give you a taste of what I’m talking about, let’s answer the question “What is a function?” We’ll start with sets, which are just collections of objects. (Like most books at this level, How to Prove It essentially follows naive set theory without worrying about the subtleties of the subject.) Given two sets, we can form their Cartesian product, which is just the set of all ordered pairs of elements.2 For example, given sets \( A = \set{1, 2, 3} \) and \( B = \set{2, 4} \), the Cartesian product is
A relation between sets \( A \) and \( B \) is just a subset of the Cartesian product \( A \cross B \):
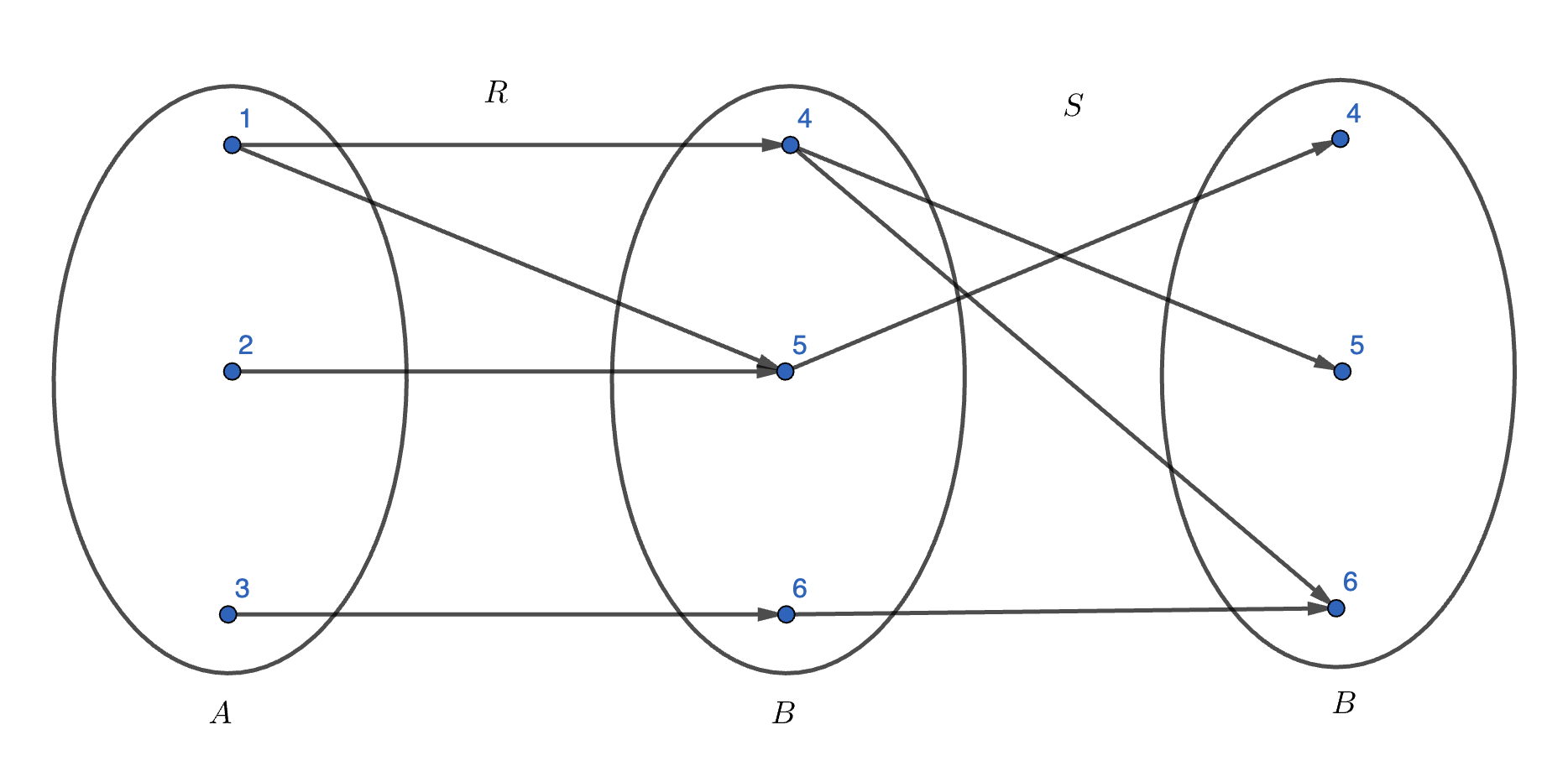
That’s it. The more intuitive idea of a relation that you may be familiar with, involving mapping points from one set to another (as in Figure 1), is an interpretation of this definition. In particular, \( R \subseteq A \cross B \) is the same as a relation \( R \) from \( A \) to \( B \). The ordered pair \( (1, 2) \) indicates that element \( 1 \) in \( A \) is associated with element \( 2 \) in \( B \).
The relations in Figure 1 actually involve the important idea of composition, which I’ve known about forever but, yet again, could not have defined rigorously until studying Velleman. Indeed, I don’t think I even knew relations could be composed; my prior experience with composition involved functions. So what is the composition of relations \( R \) from \( A \) to \( B \) and \( S \) from \( B \) to \( C \)? Here’s the rigorous definition:
If you find that hard to parse—study Velleman!
Now we get to answering the question we started with: What is a function? It’s a particular kind of relation—one where every element in \( A \) is associated with a unique element of \( B \). Specifically, if \( F \) is a relation from \( A \) to \( B, \) so that \( F \subseteq A \cross B \) by definition of relation, then \( F \) is a function if
All those lovely functions we all know about—polynomials, sines and cosines, exponentials, etc.—are special cases of this more general definition.
3 Some quibbles
I do have a few minor quibbles with How to Prove It, mostly related to the style of proof introduced. In many places, Velleman includes “scratch work” before including the main proof, while often saying things like “but we’re not going to put this motivation in the main proof.” Velleman is right that omitting such motivating details is a common practice in mathematics, but in my view it’s a terrible practice, and I was disappointed to see Velleman propagating it.
Like most mathematicians, in addition to omitting motivation, Velleman frequently omits the justifications as well. For example, he writes
Let \( x \in C \). Then clearly \( x \in (A \setminus B) \union C \).
instead of
Let \( x \in C \). Then \( x \in (A \setminus B) \union C \) by definition of union.
or even
Let \( x \in C \). Then \( x \in (A \setminus B) \lor x \in C \) by disjunction introduction, so \( x \in (A \setminus B) \union C \) by definition of union.
Speaking for myself, I find the final of these examples much easier to understand. (It requires knowing what “disjunction introduction” means, but if you don’t know that then at least you know where to start, namely, by looking up the definition of “disjunction introduction”.3 When the reason is omitted entirely, there are no such loose threads to pull on.)
Of course, the level of detail needs to be tailored somewhat to the audience, but in my experience most mathematicians severely underestimate the level of detail required for most students. “Oh, everyone can see why those steps are true,” a mathematician might say. No, they absolutely cannot, especially when just starting out, and even more especially when there are \( n \) statements chained together without a single justification among them.
We also see in the example above that a statement is asserted to be “clearly” true even though “clearly” is never a valid reason (more like proof by intimidation). Alas, this example is far from an exception, and a search in the book for “clearly” turns up 105 results (with an addition 56 for “clear” alone)—though happily not as many things are “obvious” (only 13 results). Such assertions are one of my pet peeves because they not only omit the actual reason, leading to possible confusion, they make the reader feel stupid if unable to supply it. It’s a standard practice, but an unfortunate one.
Despite these issues, overall Velleman’s “structured approach” to proofs is excellent, and students who study the book closely (and especially if they fill in the many gaps in reasoning) will come away with a world-class introduction to the subject.
4 Closing chapters
Finally, I’d like to mention how much I enjoyed the final two chapters of How to Prove It, which as far as I can tell are frequently omitted in courses that use the book. Chapter 7 includes a wonderfully economical introduction to some core ideas in number theory, culminating in a rigorous discussion of the RSA cryptosystem, which among other things underlies a large fraction of secure communications on the Internet. And Chapter 8 includes a dense4 and wonderfully rigorous5 introduction to infinite sets, including detailed subjects like equinumerosity and countability. (I love these subjects and have studied them extensively over the years, but I still learned a ton from Chapter 8.) The book ends with a detailed proof of the important Cantor–Schröder–Bernstein theorem, one of my favorite examples of a result that appears to be trivial but is actually quite deep.6
5 Conclusion
If I had to choose only one text to study, I would be inclined to pick Pure Mathematics for Beginners because of its exceptional breadth (while also covering intro to proof). But Velleman is a close second, and luckily, since I’m writing my own curriculum, I don’t have to choose between them. If you’re looking for a great foundational text with lots of problems of extraordinary depth, it’s hard to go wrong with How to Prove It by Daniel Velleman. (Just change every occurrence of “clearly <result>” to “<result> because <justification>” and it’ll be perfect.)