An AoPS Problem for Half Tau Day 2025

Happy Half Tau Day, everyone! Today on 3/14 we celebrate the halfway point ’round the unit circle, $ \tau/2 = 3.14159\ldots $

Tau, as you’ll likely recall, is the circle constant defined by the equation $ \tau = C/r $, a notation first publicly proposed by yours truly in 2010 via the now-infamous math essay The Tau Manifesto. Since radian angle measure is defined by $ \theta = s/r $, setting the arc length $ s $ equal to the full circumference $ C $ shows that $ \theta = C/r = \tau $ is the angle of a full turn of a circle. Setting $ r = 1 $, we see that, equivalently, we can think of $ \tau $ as the circumference of a unit circle. It’s all so easy and natural with $ \tau $!

In honor of this semi-auspicious day, I thought I’d share with you an exercise (and a preliminary example) from a two-volume set of books I recently finished studying: The Art of Problem Solving, Volumes 1 & 2. Though nominally aimed at high-school students, AoPS (as it’s abbreviatedly known) is full of material sufficient to challenge even quite experienced students of mathematics.

This post is long enough as it is, so I’ll assume a reasonable background in (very) elementary number theory and trigonometry. The main results we’ll need are that a sinusoid of the form $ \sin \omega x $ (or $ \cos \omega x $) has period $ T = \tau/\omega $ and that the product of two integers is equal to the product of their greatest common divisor (GCD) and least common multiple (LCM).

Even if you’d rather not follow the argument in detail, one big takeaway is how much more natural $ \tau $ is than its commonly used but inferior cousin $ \pi $. If you rewrite the argument below in terms of $ \pi $, you’ll find that there are factors of $ 2 $ everywhere—except where they cancel, which is arguably even worse. For example, the function $ f(x) = \sin 2x + \cos 3x $ combines sinusoids with periods $ \pi $ and $ 2\pi/3 $, i.e., $ 2\pi/2 $ and $ 2\pi/3 $, which is just a confusing way of writing $ \tau/2 $ (a half tau) and $ \tau/3 $ (a third tau).

This brings us to our preliminary problem, which appears as Example 2-13 in the second volume of AoPS, a.k.a. AoPSv2:

Example 2-13. Find the period of $ f(x) = \sin 2x + \cos 3x $.

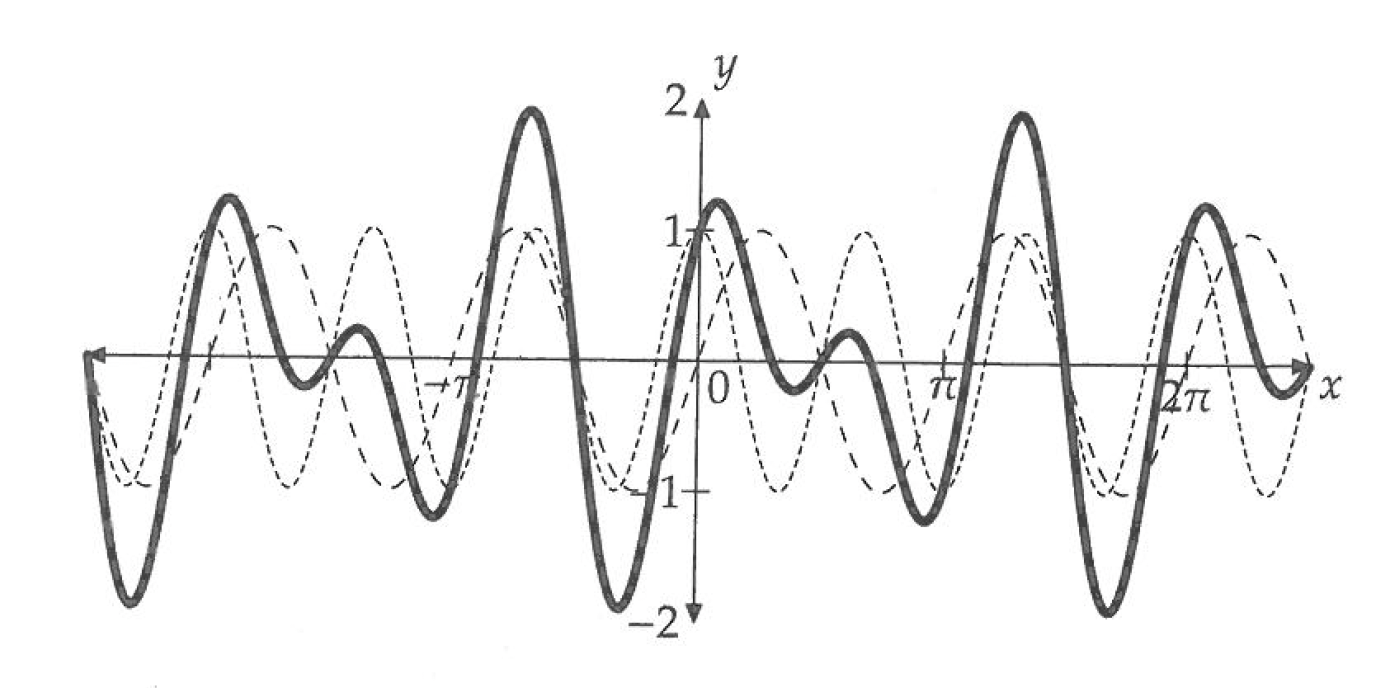
Solution: The period of $ \sin 2x $ (light dashed line in Figure 1) is $ \tau/2 $ and that of $ \cos 3x $ (light dotted line in Figure 1) is $ \tau/3 $. In one full period of length $ T $ of $ f(x) $, both $ \sin 2x $ and $ \cos 3x $ must go through an integral number of periods. (Why? Because otherwise they can’t land at the same point.) Hence, for some positive integers $ m $ and $ n $, we have $ T = m\tau/2 = n\tau/3 $. Writing this as $ n = 3m/2 $, the smallest possible solutions are $ m, n = 2, 3 $. (Why do we want the smallest solutions? Because otherwise we would be finding a quantity equal to two or more periods.) The period of $ f(x) $ is then $ T = 2\tau/2 = 3\tau/3 = \tau $.

Exercise 2-23. Extend the above argument to find the period of

\begin{equation} \label{eq:ex_2_23} \sin\left(\frac{ax}{b}\right) + \cos\left(\frac{cx}{d}\right), \end{equation}
where $ a $, $ b $, $ c $, and $ d $ are positive integers and $ a/b $ and $ c/d $ are in lowest terms.

Solution: This is exactly the kind of problem I wanted to know how to do when I started studying The Art of Problem Solving, and which (despite having a Ph.D. in physics) I couldn’t do even a few months before encountering this problem in 2024. This was due not to any deficiency in my understanding of periods of sinusoids, but rather to a weakness in my understanding of elementary number theory.

For concreteness, you may find it helpful (as I did) to have a particular example in mind; the one I used was

\begin{equation} \label{eq:period_sin_cos_complicated} \sin\left(\frac{8x}{15}\right) + \cos\left(\frac{4x}{25}\right), \end{equation}

which corresponds to Eq. (1) with $ a = 8 $, $ b = 15 $, $ c = 4 $ and $ d = 25 $. A plot of this function appears in Figure 2.

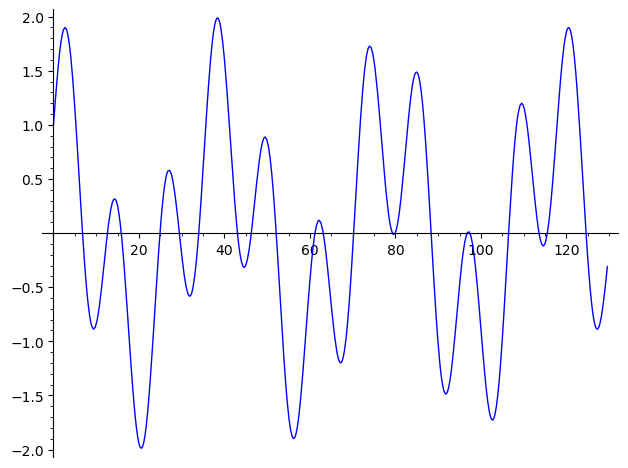
images/figures/period_sin_cos_complicated

$ \sin\left(\frac{8x}{15}\right) + \cos\left(\frac{4x}{25}\right) $.

Let’s consider the periods of the sine and cosine components of Eq. (1) separately. Since $ T = \tau/\omega $, alternately setting $ \omega = a/b $ and $ \omega = c/d $ gives $ T_\mathrm{sin} = \tau b/a $ and $ T_\mathrm{cos} = \tau d/c $. Extending the argument in Exercise 2-13, we must find the smallest pair of integers $ m $ and $ n $ satisfying $ m T_\mathrm{sin} = n T_\mathrm{cos} $, or

\[ m \tau \frac{b}{a} = n \tau \frac{d}{c}. \]

Upon canceling the factors of $ \tau $, we have

\begin{equation} \label{eq:m_and_n} m \frac{b}{a} = n \frac{d}{c}. \end{equation}

Solving Eq. (3) for $ n $ gives

\begin{equation} \label{eq:n_in_terms_of_m} n = \frac{bc}{ad}\,m. \end{equation}

By hypothesis, $ n $ is an integer, and the pairs $ a, b $ and $ c, d $ are relatively prime (since we are given that they are in lowest terms). But we are given no such assurances about the pairs $ a, c $ and $ b, d $, so to find the smallest valid value of $ n $ we must cancel any common factors.

I wouldn’t have guessed that at this point in my life I could learn more about what it means to write fractions in lowest terms, but in fact what we are doing is dividing out by the greatest common divisor (written as $ \gcd(a, b) $ or, as in AoPS, as simply $ (a, b) $). Dividing out by the GCD on the top and bottom of a fraction (which is valid since it’s equivalent to multiplying by $ 1 $), we have things like

\[ \frac{b}{c} = \frac{\frac{b}{(b, c)}}{\frac{c}{(b, c)}}. \]

By definition of GCD, $ b/(b, c) $ and $ c/(b, c) $ are both integers, which is why this trick is useful. In particular, we can do the same thing to all the terms in Eq. (4) and express the fraction in terms of the common divisors:

\begin{align*} n & = \frac{bc}{ad}\,m \\ & = \frac{\frac{b}{(b, d)}\cdot\frac{c}{(a, c)}}{\frac{d}{(b, d)}\cdot\frac{a}{(a, c)}}\,m. \end{align*}

At this point, we have written the fraction in lowest terms by definition,¹ so we can read off the values of $ m $ that makes $ n $ an integer, which happens when $ m $ is an integral multiple of the denominator:

\[ m_k = k \cdot \frac{d}{(b, d)}\cdot\frac{a}{(a, c)} \]

for positive integer $ k $. This way, $ m_k $ cancels the denominator of $ n $,

\[ \frac{d}{(b, d)}\cdot\frac{a}{(a, c)}, \]

ensuring that $ n $ is an integer as required. In particular, the smallest value of $ m_k $ occurs when $ k = 1 $, corresponding to the point where the combined function has gone through one period. In this case, $ m = m_1 $ is equal to the denominator itself, so that

\[ m = 1 \cdot \frac{d}{(b, d)}\cdot\frac{a}{(a, c)} = \frac{d}{(b, d)}\cdot\frac{a}{(a, c)}. \]

Plugging this value into Eq. (3) then gives

\begin{align*} T & = m \frac{b}{a}\,\tau \\ & = \frac{d}{(b, d)}\cdot\frac{a}{(a, c)}\cdot\frac{b}{a}\,\tau & & \text{Substitution for $m$} \\ & = \frac{bd}{(b, d)}\cdot\frac{1}{(a, c)}\,\tau. & & \text{Canceling common factor $a$} \end{align*}

Now, as shown in Chapter 5 of AoPSv1, we have the following important result involving the GCD and LCM:

The product of two integers is equal to the product of their greatest common devisor and least common multiple.

The LCM is typically written as $ \mathrm{lcm}(b, d) $ or, as in AoPS, as $ [b, d] $. Following this latter convention, the result just mentioned takes the form

\[ bd = (b, d)[b, d], \]

and hence we can write

\begin{align*} T & = \frac{bd}{(b, d)}\cdot\frac{1}{(a, c)}\,\tau \\ & = \frac{(b, d)[b, d]}{(b, d)}\cdot\frac{1}{(a, c)}\,\tau & & \text{Substitution for $bd$} \\ & = \frac{[b, d]}{(a, c)}\,\tau. & & \text{Canceling common factor $(b, d)$} \end{align*}

Thus, we have found that a sum of sinusoids of the form

\begin{equation} \label{eq:sum_of_sinusoids} \sin\left(\frac{ax}{b}\right) + \cos\left(\frac{cx}{d}\right) \end{equation}

for positive integers $ a, b, c, d $ has period $ T $ given by

\begin{equation} \label{eq:period_sin_cos} T = \frac{[b, d]}{(a, c)}\,\tau, \end{equation}

where $ [b, d] $ is the least common multiple of $ b $ and $ d $ and $ (a, c) $ is the greatest common divisor of $ a $ and $ c $.

Comparing Eq. (5) to the problem from Example 2-13 yields $ a = 2 $, $ b = 1 $, $ c = 3 $, $ d = 1 $, so applying Eq. (6) gives

\[ T = \frac{[1, 1]}{(2, 3)}\,\tau = \frac{1}{1}\,\tau = \tau \]

as required.

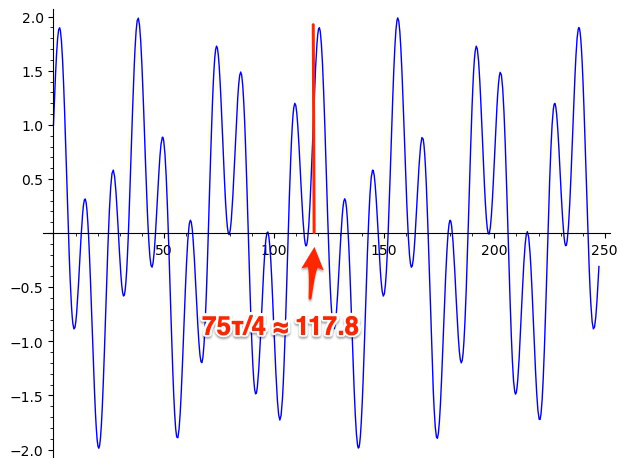
images/figures/period_sin_cos_complicated_labeled

Just over two periods of $ \sin\left(\frac{8x}{15}\right) + \cos\left(\frac{4x}{25}\right) $.

Applying Eq. (6) to the more complicated case in Eq. (2), we have $ a = 8 $, $ b = 15 $, $ c = 4 $, and $ d = 25 $. To fill in the terms in Eq. (6), we need $ [b, d] = [15, 75] $ and $ (a, c) = (4, 8) $. The least common multiple of $ 15 $ and $ 25 $ is $ 75 $ and the greatest common divisor of $ 4 $ and $ 8 $ is $ 4 $, so using Eq. (6) we find that the period of

\[ \sin\left(\frac{8x}{15}\right) + \cos\left(\frac{4x}{25}\right) \]

\[ T = \frac{[b, d]}{(a, c)}\,\tau = \frac{[15, 25]}{(4, 8)}\,\tau = \frac{75}{4}\tau. \]

Noting that $ 75\tau/4 \approx 117.8 $, we see that this result agrees nicely with the plot shown in Figure 3.

It would be exceptionally difficult to “eyeball” the function in Eq. (5) to determine its period by inspection, but with Eq. (6) in hand we can calculate it quite easily. (All we need are algorithms to calculate the LCM and calculate the GCD, which are well-known.) And since the LCM and GCD are both integers, the period $ T $ is always a rational multiple of $ \tau $.

1. I did not realize until I solved this problem that this can be taken as the rigorous definition of “lowest terms”.